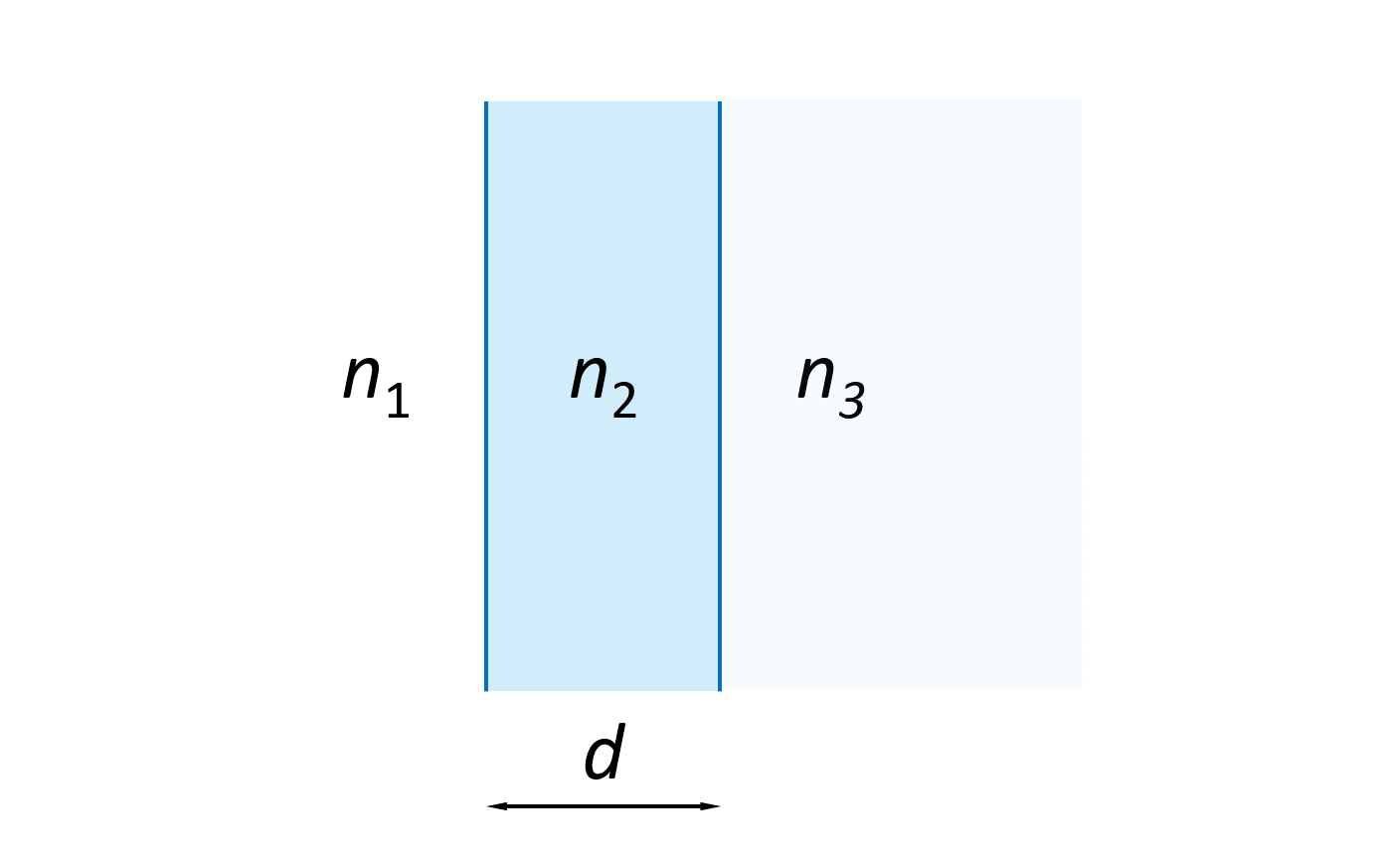Lernen Sie die Grundlagen von optischen dielektrischen Mehrschichtfiltern kennen
Wie funktioniert ein Interferenzfilter?
Interferenzfilter sind sehr effektiv, um fast jede Art von spektraler optischer Filterung zu erreichen. Typische Beispiele sind Kurzwellen-, Langwellen- und Bandpassfilter. Aber auch komplexere Filter wie Multibandpassfilter, kontinuierlich variable Filter und dichroitische Filter können eingesetzt werden. Einer der Hauptvorteile von Interferenzfiltern ist, dass nahezu jede spektrale Filterfunktion entworfen und implementiert werden kann. Ein Interferenzfilter besteht aus einem flachen Substrat (häufig Glas) mit vielen dünnen Beschichtungen aus dielektrischen Materialien auf einer oder beiden Seiten des Substrats. Die Beschichtungen wechseln zwischen einem Material mit hohem und niedrigem Brechungsindex ab. In diesem technischen Hinweis werden die Grundlagen der Funktionsweise eines Interferenzfilters erläutert.
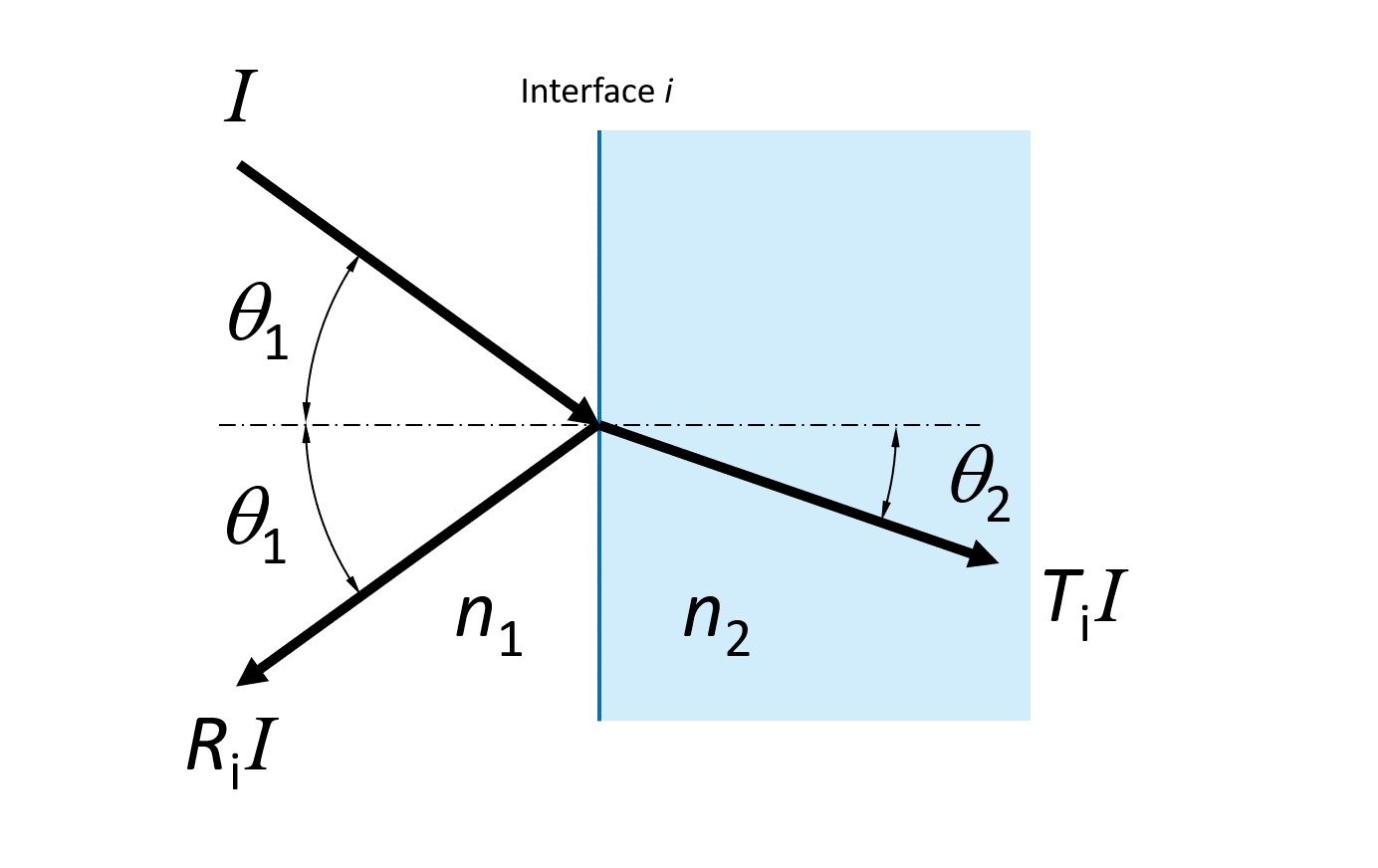
Grenze zwischen zwei dielektrischen Schichten
Bevor untersucht wird, wie die dielektrischen Schichten einen Interferenzfilter bilden, ist es sinnvoll, die Grenze zwischen zwei Schichten zu betrachten.
Wenn Licht auf die Grenzfläche (mit i gekennzeichnet) fällt, wird ein Teil (Ri) der Lichtintensität reflektiert und ein Teil (Ti) durchgelassen. Wenn wir davon ausgehen, dass die Grenzfläche verlustfrei ist, was eine gute Näherung für Dielektrika ist, diktiert die Energieerhaltung Folgendes:
Ti = 1 – Ri
Das Verhältnis zwischen dem Winkel des einfallenden und des durchgelassenen Lichts im Verhältnis zur Normalen wird durch das Snellsche Brechungsgesetz bestimmt:
n1 sin(θ1) = n2 sin(θ2)
Die Reflexions- und Transmissionskoeffizienten (Intensität) sind für s- und p-polarisiertes Licht unterschiedlich und hängen wie folgt von den Brechungsindizes und dem Einfallswinkel ab:
| Rs = ( |
|
)2 |
Ts = 1 – Rs
| Rs = ( |
|
)2 |
Tp = 1 – Rp
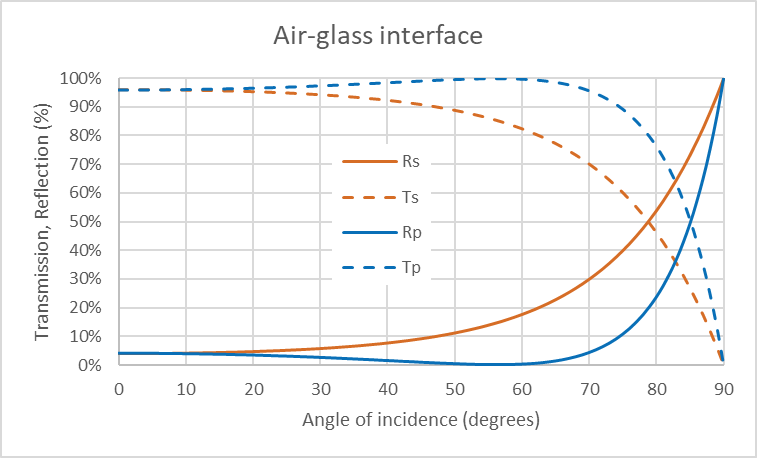
Für die Grenzfläche zwischen Luft (n1 = 1) und Glas (n2 = 1,5) sind die Reflexions- und Transmissionskoeffizienten für s- und p-polarisiertes Licht in Abhängigkeit vom Einfallswinkel in Abbildung 3 dargestellt.
Einzelne dielektrische Schicht
Bei Interferenzfiltern werden oft Hunderte von Schichten verwendet, aber um die Grundlagen zu verstehen, betrachten wir nur eine einzelne dielektrische Schicht, wie in Abbildung 4 dargestellt. Die dielektrische Schicht hat eine Dicke d und einen Brechungsindex n2 und ist umgeben von einem Medium mit dem Brechungsindex n1 links und n3 rechts.
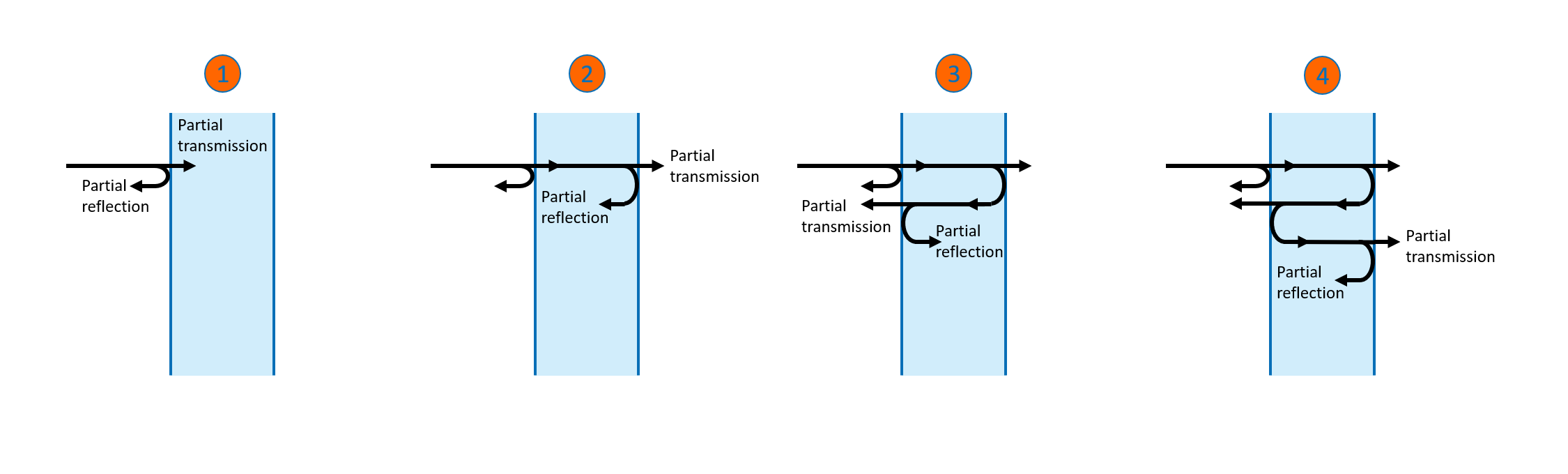
Wenn Licht von links auf die Oberfläche der dielektrischen Schicht auftrifft, wird ein Teil des Lichts durch die Oberfläche hindurchgelassen, und das restliche Licht wird reflektiert, wie in Zeichnung 1 in Abbildung 5 dargestellt. Die Zeichnungen 2 bis 4 veranschaulichen, wie das in die dielektrische Schicht eingedrungene Licht zwischen den beiden Oberflächen reflektiert und bei jedem Sprung ein gewisser Teil des Lichts durch die Oberfläche übertragen wird. Abbildung 5 zeigt nur die ersten paar Reflexionen, aber es findet eine unendliche Anzahl von Reflexionen und Übertragungen statt.
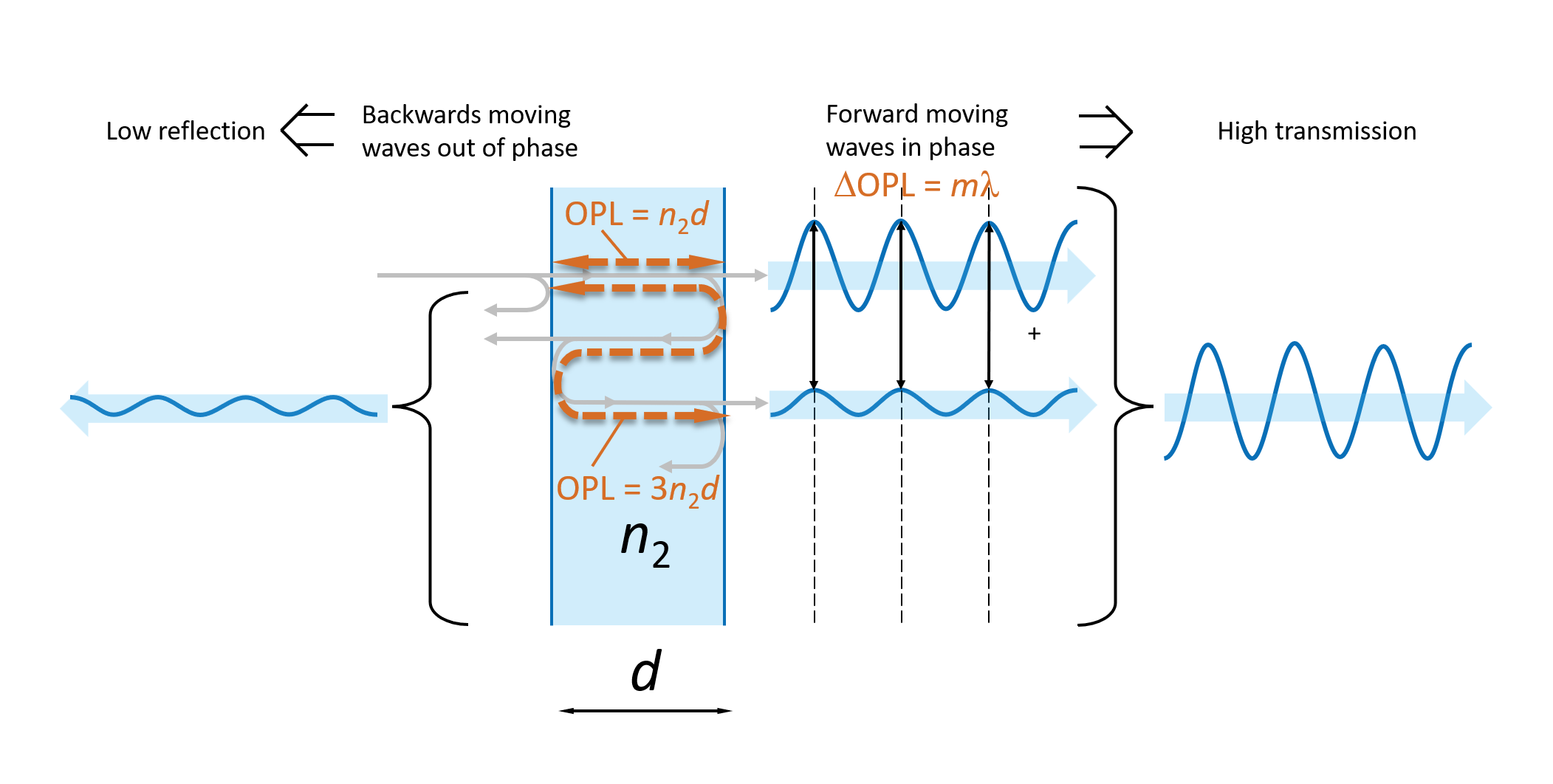
Auf jeder Seite der dielektrischen Schicht ergibt sich eine Summe der durchgelassenen (sich vorwärts bewegenden) Wellen und eine Summe der reflektierten (sich rückwärts bewegenden) Wellen. Wenn die sich vorwärts bewegenden Wellen alle in Phase sind, wie in Abbildung 6 dargestellt, addieren sich die Wellen, um ein Maximum an durchgelassenem Licht durch die dielektrische Schicht zu erzeugen. Folglich sind die sich rückwärts bewegenden Wellen phasenverschoben, und es wird eine minimale Lichtmenge reflektiert.
Damit die sich vorwärts bewegenden Wellen alle in Phase sind, muss die Differenz zwischen der optischen Weglänge (OPL), die jede Welle beim Durchlaufen der dielektrischen Schicht erfährt, eine ganzzahlige Anzahl m von Wellenlängen λ betragen. Dies kann wie folgt geschrieben werden:
ΔOPL = mλ
Die optische Weglänge ist gleich der in einem Medium zurückgelegten Strecke multipliziert mit dem Brechungsindex des Mediums. Dies bedeutet, dass die OPLs für die direkt übertragene und die erste doppelt reflektierte Welle durch die dielektrische Schicht (siehe Abbildung 6) wie folgt sind:
OPL(direkt transmittiert) = n2d
OPL(doppelt reflektiert) = 3n2d
und daher
ΔOPL = 2n2d
In dem Fall, in dem wir eine maximale Transmission durch die dielektrische Schicht wünschen, sollte ΔOPL einer ganzzahligen Anzahl von Wellenlängen entsprechen (ΔOPL = mλ), was bedeutet, dass für eine maximale Transmission die Dicke der Schicht die folgende Bedingung erfüllen sollte:
d = mλ / 2n2
Aus dieser Analyse können wir auch schließen, dass bei einer gegebenen Dicke und einem gegebenen Brechungsindex einer dielektrischen Schicht eine maximale Transmission bei den folgenden Wellenlängen erreicht wird:
λpeak = 2n2d / m
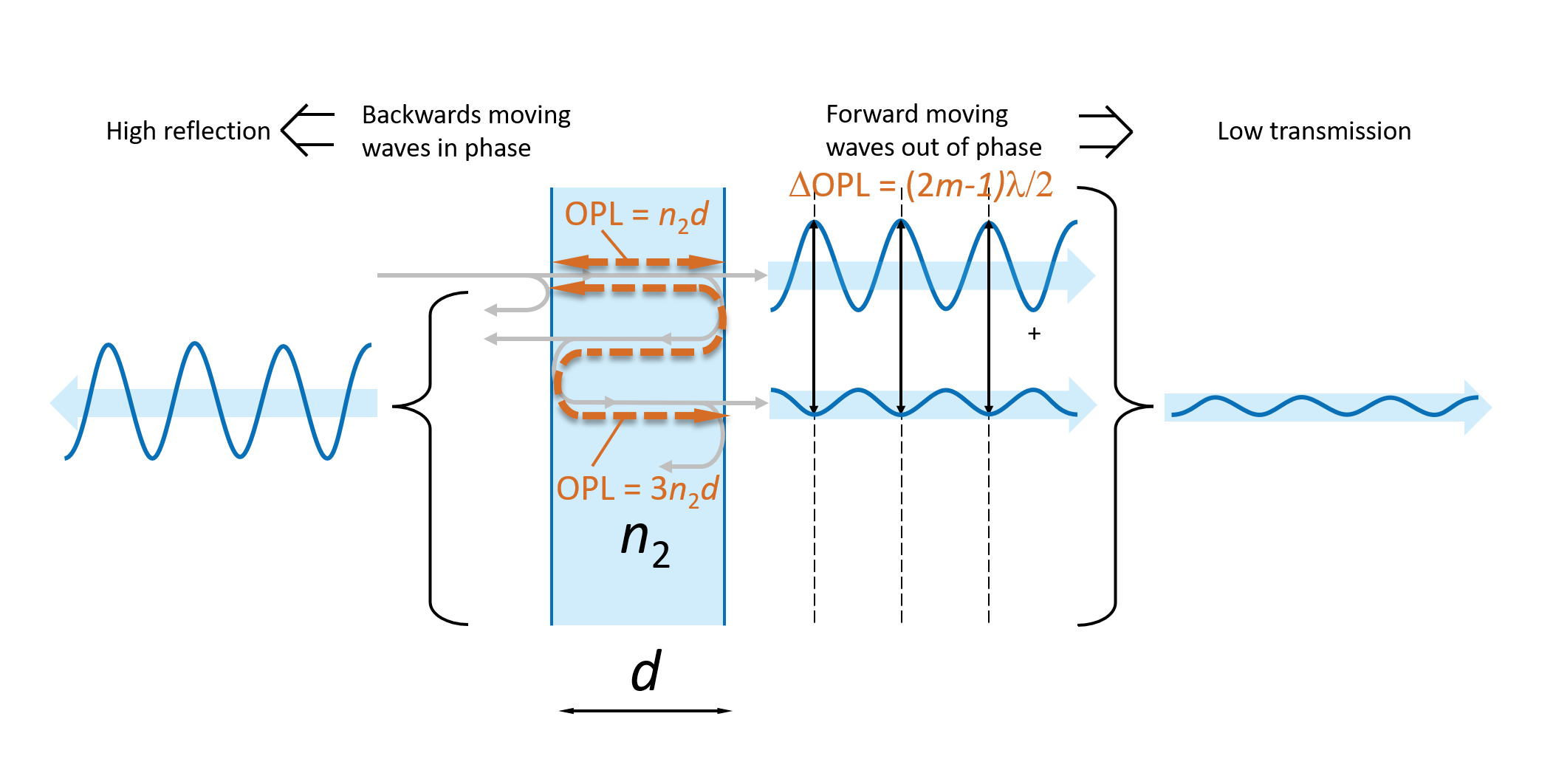
In dem Fall, in dem sich die vorwärtslaufenden Wellen phasenverschoben addieren, entsprechen die optischen Weglängendifferenzen einer ungeraden Anzahl von Halbwellenlängen:
ΔOPL = (2m-1)λ / 2
wie in Abbildung 7 dargestellt.
Das tatsächliche Maximum und Minimum des durchgelassenen Lichts hängt vom Reflexionskoeffizienten Ri an jeder der beiden Oberflächen i = I bzw. II ab. Für den Fall, dass n1 = n3, werden die beiden Reflexionskoeffizienten identisch, also RI = RII = R. In diesem vereinfachten Fall kann gezeigt werden, dass die Gesamttransmission Ttot durch die folgende Gleichung gegeben ist:
| Ttot = |
|
Dabei wird das Pluszeichen im Nenner verwendet, wenn n2 < n1 ist, und das Minuszeichen, wenn n2 > n1 ist.
Laden Sie dieses Whitepaper herunter
Nutzen Sie diese Gelegenheit, um Ihr Wissen zu erweitern und Ihre Forschung zu beschleunigen.
Laden Sie dieses aktuelle Whitepaper herunter
Mehrschichtige Beschichtungen
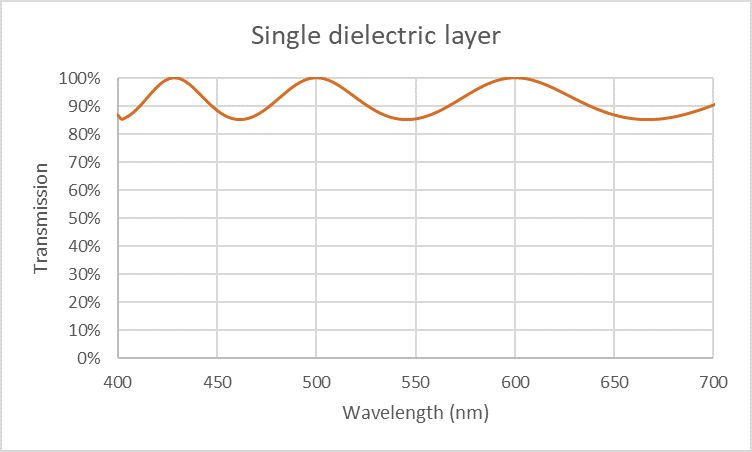
Wie soeben beschrieben, ergibt eine einzige dielektrische Beschichtung einen optischen Filter mit maximaler Transmission bei den Wellenlängen, die durch λpeak = 2n2d / m, gegeben sind, wobei m eine ganze Zahl ist. Die spektrale Transmission eines solchen Filters ist in Abbildung 8 für den Fall dargestellt, dass d = 1 µm und n2 = 1.5 und die Reflexion R an jeder Oberfläche 4 % beträgt. Obwohl das Filter erwartungsgemäß maximale und minimale Transmissionen liefert, ist es kein sehr nützliches Filter.
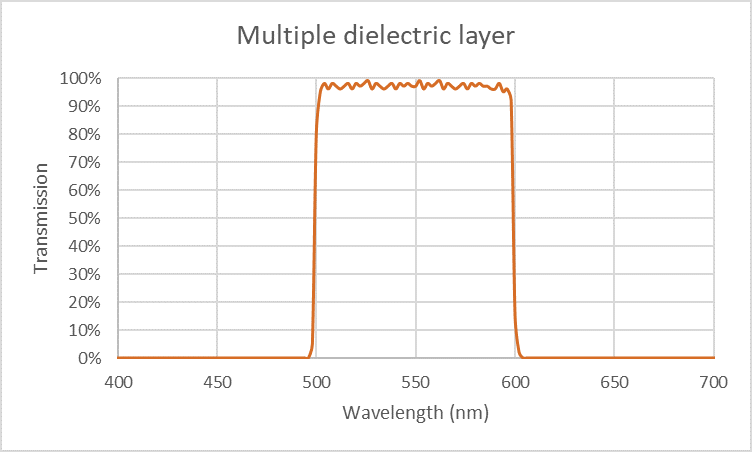
Eine gängige Filterfunktion sind Antireflexionsbeschichtungen (AR), die die Reflexion an der Luft-Glas-Grenzfläche verringern und dadurch die Transmission verbessern. Eine einfache AR-Beschichtung kann mit einer einzigen Schicht aus MgF2 hergestellt werden, die einen Brechungsindex von etwa 1,38 und eine Dicke von λ/4 hat. Mit einer solchen MgF2-Schicht kann die Reflexion von 4 % auf etwa 1 % reduziert werden. Um fortschrittlichere Filter zu entwerfen, ist es notwendig, viele dielektrische Schichten mit abwechselnd hohem und niedrigem Brechungsindex hinzuzufügen. Auf diese Weise ist es möglich, einen Bandpassfilter wie in Abbildung 9 mit einer hohen Transmission im Durchlassband und einer starken Unterdrückung außerhalb des Durchlassbandes herzustellen. Andere gebräuchliche Arten von optischen Filtern sind Kantenfilter, Notchfilter und Strahlenteiler für Intensität, Wellenlänge oder Polarisation. Darüber hinaus können noch fortschrittlichere Filter hergestellt werden, indem mehrere Filterfunktionen in derselben Beschichtung kombiniert werden. Ein Beispiel dafür sind Multibandpassfilter, die mehrere Wellenlängenbereiche in einem Filter durchlassen.
Mehr erfahren
Delta Optical Thin Film verfügt über mehr als 50 Jahre Erfahrung in der Entwicklung und Herstellung von hochentwickelten Interferenzfiltern. Wir haben Pionierarbeit bei vielen innovativen Lösungen geleistet, die heute häufig in analytischen Instrumenten eingesetzt werden. Stöbern Sie auf unseren Produktseiten in den vielen Beispielen für Produkte, die wir hergestellt haben.
Bleiben Sie auf dem Laufenden mit unserem Expertenwissen
Erhalten Sie die neuesten Nachrichten und Erkenntnisse über optische Filter – abonnieren Sie unseren Newsletter.